Підготовка до ЗНО з математики. Алгебра.

    Приклад 10. Розв’яжіть систему нерівностей 

$\left\{ \begin{array}{l}5x + 6 \le x,\\3x + 12 \le x + 17.\end{array} \right.$

Розв’язання

     Маємо 

$\left\{ \begin{array}{l}5x - x \le - 6,\\3x - x \le 17 - 12;\end{array} \right.\quad \left\{ \begin{array}{l}4x \le - 6,\\2x \le 5;\end{array} \right.\quad \left\{ \begin{array}{l}x \le 1,5,\\x \le 2,5.\end{array} \right.$

     Зображаємо на числовій прямій множини розв’язків кожної з нерівностей

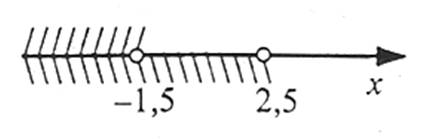
     Обидві нерівності справедливі при х≤-1,5. Відповідь можна записати у вигляді нерівності х≤-1,5 або у вигляді числового проміжку (-∞;-1,5].

     Відповідь: (-∞;-1,5].

    Приклад 11. Розв’яжіть систему нерівностей 

$\left\{ \begin{array}{l}17x - 2 > 12x - 1,\\3 - 9x < 1 - x.\end{array} \right.$

Розв’язання

     Маємо 

$\left\{ \begin{array}{l}17x - 12x > 2 - 1,\\ - 9x + x < - 3 + 1;\end{array} \right.\quad \left\{ \begin{array}{l}5x > 1,\\ - 8x > - 2;\end{array} \right.\quad \left\{ \begin{array}{l}x > \frac{1}{5};\\x > \frac{1}{4}.\end{array} \right.$

     Використовуючи числову пряму, знайдемо спільні розв’язки нерівностей $x > \frac{1}{5}$ і $x > \frac{1}{4}$.

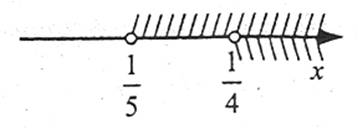
     Бачимо, що множина розв’язків системи складається із чисел, які задовольняють умові $x > \frac{1}{4}$, тобто є числовим проміжком $(\frac{1}{4}; + \infty )$.

     Відповідь: $(\frac{1}{4}; + \infty )$.

    Приклад 12. Розв’яжіть систему нерівностей 

$\left\{ \begin{array}{l}1 - 12x < 3x + 1,\\2 - 6x > 4 + 4x.\end{array} \right.$

Розв’язання

     Маємо 

$\left\{ \begin{array}{l} - 12x - 3x < - 1 + 1,\\ - 6x - 4x > 4 - 2;\end{array} \right.\quad \left\{ \begin{array}{l} - 15x < 0,\\ - 10x > 2;\end{array} \right.\quad \left\{ \begin{array}{l}x > 0,\\x < - 0,2.\end{array} \right.$

     Використовуючи числову пряму, знаходимо, що спільних розв’язків нерівності х>0 і х<-0,2 не мають. Отже, дана система розв’язків не має.

     Відповідь: розв’язків не має.

    Приклад 13. Розв’яжіть систему нерівностей 

$\left\{ \begin{array}{l}2(x + 1) + 5 > 3 - (1 - 2x),\\5(x + 2) - x > 3(x - 1) + x.\end{array} \right.$

Розв’язання

     Маємо 

$\left\{ \begin{array}{l}2x + 2 + 5 > 3 - 1 + 2x,\\5x + 10 - x > 3x - 3 + x;\end{array} \right.\quad \left\{ \begin{array}{l}2x - 2x > - 2 - 5 + 3 - 1,\\5x - x - 3x - x > - 10 - 3;\end{array} \right.\quad \left\{ \begin{array}{l}0x > - 5,\\0x > - 13.\end{array} \right.$

     Розв’язком першої і другої нерівностей є числова пряма (-∞;+∞). Отже, розв’язком даної системи є будь-яке число х.

     Відповідь: (-∞;+∞).

    Приклад 14. Розв’яжіть нерівність (х-3)(2-х)≥0.

Розв’язання

     Добуток двох множників невід’ємний, коли обидва множники або невід’ємні, або недодатні. Тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей:

$\left\{ \begin{array}{l}x - 3 \ge 0,\\2 - x \ge 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}x - 3 \le 0,\\2 - x \le 0.\end{array} \right.$

     Тоді маємо:  

$\left\{ \begin{array}{l}x \ge 3,\\x \le 2\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}x \le 3,\\x \ge 2.\end{array} \right.$

     Оскільки перша система не має розв’язків, а розв’язком другої системи є проміжок [2;3], то дана система має множину розв’язків – [2;3].

     Відповідь: [2;3].

    Приклад 15. Розв’яжіть нерівність $\frac{{x + 1}}{{x - 1}} < 0$.

Розв’язання

     Дріб від’ємний, коли значення чисельника і знаменника мають протилежні знаки, тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей:

$\left\{ \begin{array}{l}x + 1 > 0,\\x - 1 < 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}x + 1 < 0,\\x - 1 > 0.\end{array} \right.$

     Тоді маємо:  

$\left\{ \begin{array}{l}x > - 1,\\x < 1\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}x < - 1,\\x > 1.\end{array} \right.$

     Оскільки друга система не має розв’язків, а розв’язком першої системи є проміжок (-1;1), то дана система має множину розв’язків – (-1;1).

     Відповідь: (-1;1).