Підготовка до ЗНО з математики. Алгебра.

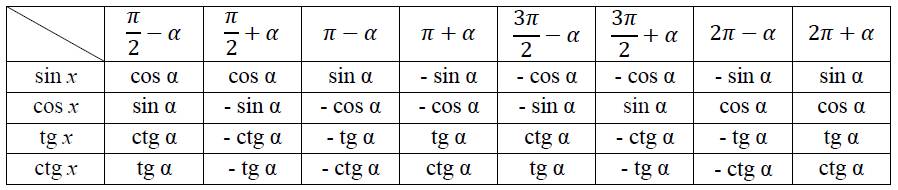
     Формули зведення запам’ятовувати необов’язково. Для того, щоб записати будь-яку з них, можна користуватися таким правилом:

1. у правій частині формули ставиться той знак, який має ліва частина при умові $0 < \alpha < \frac{\pi }{2}$;

2. якщо в лівій частині формули кут дорівнює $\frac{\pi }{2} \pm \alpha ,\frac{{3\pi }}{2} \pm \alpha$, то синус замінюється на косинус, тангенс – на котангенс і навпаки. Якщо кут дорівнює π±α, то заміна не виконується.

     Розглянемо приклади.

     Приклад 2. Виразимо tg (π-α) через тригонометричну функцію кута α. Якщо вважати, що α – кут І чверті, то π-α буде кутом ІІ чверті. У ІІ чверті тангенс від’ємний, отже, у правій частині рівності слід поставити знак «мінус». Для кута π-α назва функції «тангенс» зберігається. Тому

tg (π-α)=-tg α.

     За допомогою формул зведення знаходжень значень тригонометричних функцій будь-якого числа можна звести до знаходження значень тригонометричних функцій чисел від 0 до .

    Приклад 3. Знайдіть значення $\sin \frac{\pi }{3}$.

     Маємо: $\sin \frac{\pi }{3} = \sin (2\pi + \frac{{2\pi }}{3}) = \sin \frac{\pi }{3} = \sin (\pi - \frac{\pi }{3}) = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}$.