Підготовка до ЗНО з математики. Алгебра.

     Показниковими називаються рівняння, в яких невідоме міститься в показнику степеня при сталих основах.

     Наприклад: рівняння ${2^x} + 3 = 0;\;{3^{x + 1}} - {3^x} - 1 = 0$ є показниковими.

      Найпростішим показниковими рівнянням є рівняння ${a^x} = b,a > 0,a \ne 1$.

     Оскільки множина значень функції $y = {a^x}$ - множина додатних чисел, то рівняння ${a^x} = b$:

1)               має один корінь, якщо b>0;

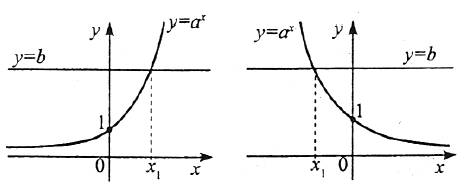
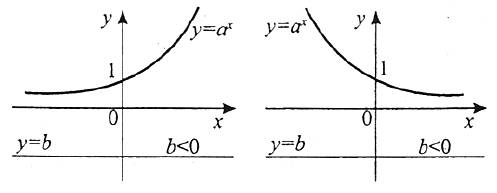
2)               не має коренів, якщо b≤0.

    Для того, щоб розв’язати рівняння ${a^x} = b,a > 0,a \ne 1,\;b > 0$, треба b подати у вигляді $b = {a^c}$, тобі будемо мати ${a^x} = {a^c}$, звідси х=с.

     Розглянемо приклади.

     Приклад 1. Розв’яжіть рівняння .${5^x} = 125$

Розв’язання

     Оскільки ${5^x} = 125$, а $125 = {5^3}$, то маємо ${5^x} = {5^3}$, звідси х=3.

     Відповідь: 3.

     Приклад 2. Розв’яжіть рівняння ${(\frac{1}{7})^x} = 49$.

Розв’язання

     Оскільки $49 = {7^2} = {(\frac{1}{7})^{ - 2}}$, то маємо ${(\frac{1}{7})^x} = {(\frac{1}{7})^{ - 2}}$, звідси х=-2.

     Відповідь: -2.

     Приклад 3. Розв’яжіть рівняння ${15^{{x^2} - 5x + 6}} = 1$.

Розв’язання

     Оскільки ${15^0} = 1$, то ${15^{{x^2} - 5x + 6}} = {15^0},\;{x^2} - 5x + 6 = 0$, звідси х₁=2, х₂=3.

     Відповідь: 2; 3.