Показникова функція. Показникові рівняння, нерівності та їх системи
3. Деякі способи розв’язування показникових рівнянь
І спосіб. Приведення рівняння до спільної основи, тобто до рівняння  .
.
Як відомо, показникова функція  монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності випливає, що f(x)=g(x).
монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності випливає, що f(x)=g(x).
ІІ спосіб. Винесення спільного множника за дужки.
ІІІ спосіб. Приведення рівняння до квадратного.
IV спосіб. Графічний спосіб роз взування показникових рівнянь.
Приклад 1. Розв’яжіть графічно рівняння  .
.
Розв’язання
Побудуємо графіки функцій  в одній системі координат. Графіки функцій
в одній системі координат. Графіки функцій  і
і  перетинаються в точці, абсциса якої х=0.
перетинаються в точці, абсциса якої х=0.
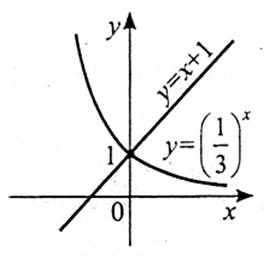
Відповідь: 0.
Зауваження. Корінь цього рівняння легко знайти усно, однак треба пам’ятати, що в цьому випадку необхідно доводити той факт, що знайдений корінь єдиний.