Початки теорії ймовірності
Операції над подіями.Теорема про ймовірність суми подій. Теорема про ймовірність добутку подій
1. Операції над подіями
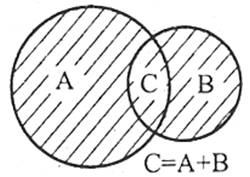
Сумою двох подій А і В називається подія , що полягає у здійсненні під час одиничного випробування або події А, або події В, або обох подій А і В одночасно (позначається С=А+В, або ![]() .
.
Подія ![]() називається протилежною події А, якщо вона відбувається тоді і тільки тоді, коли подія А не відбувається.
називається протилежною події А, якщо вона відбувається тоді і тільки тоді, коли подія А не відбувається.
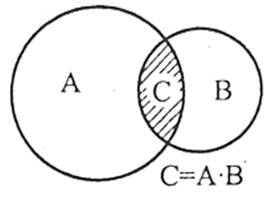
Добутком двох подій А і В називається подія С, яка полягає в одночасному здійсненні обох подій А і В під час одиничного випробування (позначається ![]() або
або ![]() .
.
2. Теорема про ймовірність суми подій
Імовірність суми двох несумісних подій А і В дорівнює сумі ймовірностей цих подій. Якщо ![]() , то Р(А+В)=Р(А)+Р(В).
, то Р(А+В)=Р(А)+Р(В).
Наприклад. Якщо спортсмен стріляє по мішені, яка розділена на 2 частини, і ймовірність попадання в першу частину дорівнює 0,45, а в другу – 0,35, то йовірність попадання в мішень становитиме 0,45+0,35=0,8.
Із теореми випливають наслідки.
Наслідок 1. Сума ймовірностей подій А1,А2,…,An, які утворюють повну групу і попарно несумісні, дорівнює 1
Р(А1)+Р(А2)+…+Р(Аn)=1.
Наслідок 2. Сума ймовірностей протилежних подій дорівнює 1
![]() .
.
3. Теорема про ймовірність добутку подій
Дві події називаються незалежними, якщо ймовірність появи однієї з них не залежить від того, відбулася інша подія чи ні.
Імовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій, тобто ![]() .
.
Якщо подія А1, А2, …Аn незалежні, то ймовірність здійснення принаймні однієї з них С може бути виражена через імовірність цих подій формулою
![]() .
.