Підготовка до ЗНО з математики. Алгебра.

Метод інтервалів

     Щоб розв’язати нерівність , де  , де – різні числа, треба:

1. зобразити 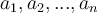 на координатній прямій (ці числа, розташовані у порядку зростання, розділяють пряму на  проміжків, на яких функція f(x) зберігає свій знак);
2. визначити знаки функції f(x) на кожному проміжку;
3. записати відповідь.

     Наприклад:  .

.

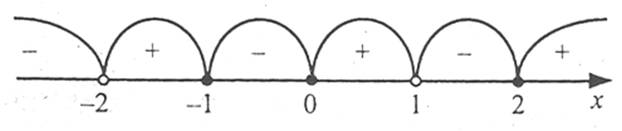
Відповідь: .

Узагальнений метод інтервалів

     Щоб розв’язати нерівність , треба:

1. знайти область визначення функції у=f(x);
2. знайти нулі функції (f(x)=0);
3. на координатній прямій позначити нулі функції і визначити знак функції на кожному проміжку, на які розбивають нулі функції область визначення;
4. записати відповідь (вибрати ті інтервали, де функція має потрібний знак).

Графічний метод

     Щоб розв’язати нерівність f(x)>g(x), треба побудувати графіки функцій y=f(x), y=g(x) і вибрати ті проміжки осі абсцис, на яких графік функції y=f(x)розташований вище графіка функції y=g(x).

     Щоб розв’язати нерівність f(x)<g(x), треба побудувати графіки функцій y=f(x), y=g(x) і вибрати ті проміжки осі абсцис, на яких графік функції y=f(x)розташований нижче графіка функції y=g(x).

     Наприклад: .

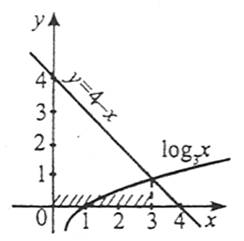
Відповідь: .