Підготовка до ЗНО з математики. Геометрія.

1. Поняття вектора

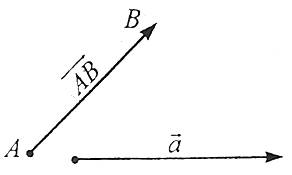
Вектор – напрямлений відрізок певної довжини, у якого один кінець вважається початком вектора, а інший – кінцем вектора.

Вектори позначаються двома великими латинським літерами зі стрілкою над ними або однією маленькою латинською літерою зі стрілкою над нею.

Наприклад: вектор   (А – початок вектора, В – кінець вектора) та вектор .

2. Координати вектора

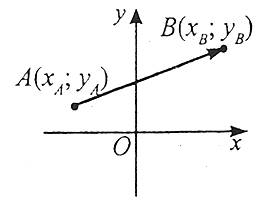
Координати вектора , що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.

Координати вектора на площині

Якщо початком вектора є точка А(х_А;у_А), а кінцем – точка В(х_В;у_В), то

.

3. Довжина вектора

 Довжина вектора (абсолютна величина, або модуль) – довжина відрізка, що зображує вектор. Позначення: .

Довжина вектора на площині

Якщо є вектор , то , де  – модуль вектора,   – його координати.

4. Рівні вектори

Рівні вектори – вектори, які мають однаковий напрямок і рівні довжини.

Наприклад: рівні вектори . Позначення: .

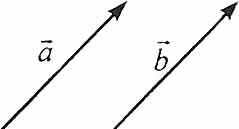
Рівні вектори мають рівні координати. Якщо координати векторів рівні, то вектори рівні.

Рівність векторів на площині

Якщо , то

.

Якщо 

, то .

 5. Протилежні вектори

Протилежні вектори – вектори, які мають протилежні напрямки і рівні довжини.

Наприклад: протилежні вектори . Позначення: .

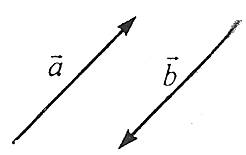
Протилежні вектори мають протилежні відповідні координати. Якщо відповідні координати двох векторів протилежні, то вектори протилежні.

Протилежні вектори на площині

Якщо маємо  і , то 

Якщо маємо  і

 , то .

6. Сума векторів

Нехай дано два вектори .

Візьмемо довільну точку А і побудуємо вектор , що дорівнює . Від точки В відкладемо вектор  , що дорівнює .

Сумою векторів  є вектор , тобто вектор, що з’єднує початок першого вектора з кінцем другого вектора (так зване правило трикутника).

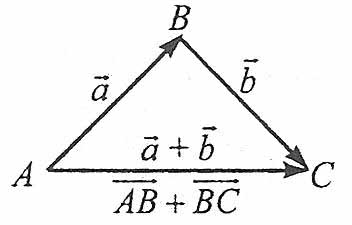
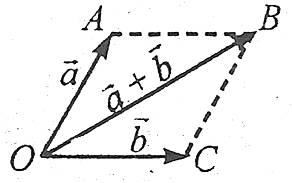
Для двох векторів (ОА і ОС) зі спільним початком (О) їхня сума зображується діагоналлю паралелограма (ОВ), побудованого на цих векторах, до того ж початок вектора-суми збігається з початком цих векторів.

Сума векторів на площині

7. Різниця векторів

Різницею векторів   є вектор , тобто вектор, що з’єднує кінці векторів  і  і напрямлений від від’ємника до зменшуваного.

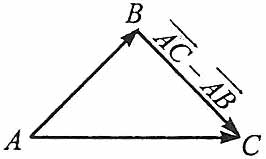
Координати різниці двох векторів дорівнюють різниці відповідних координат вектора – зменшуваного і вектора – від’ємника.

Різниця векторів на площині

8. Множення вектора на число

Добуток   вектора  на число  є вектор , а напрямок – такий самий, що й вектора , якщо , або протилежний напрямку вектора , якщо .

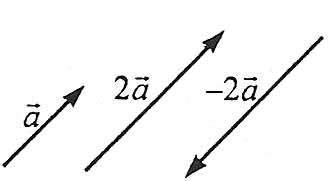
Якщо  або  , то . Координати вектора   дорівнюють добутку числа  на відповідні координати вектора .

Множення вектора на число на площині

9. Колінеарні вектори

Два ненульові вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

Наприклад: вектори  – колінеарні.

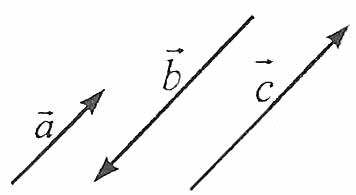
Якщо вектори колінеарні, то їхні відповідні координати пропорційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.

Колінеарність векторів на площині

Якщо є вектори  і вони колінеарні, то .

Якщо є вектори  і , то  – колінеарні вектори.

 10. Скалярний добуток двох векторів

Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів. Позначення таке саме, як і для добутку чисел, – .

Скалярний добуток двох векторів на площині

Якщо є вектори , то .

Теорема. Скалярний добуток двох векторів  дорівнює добутку довжин цих векторів на косинус кута між ними.

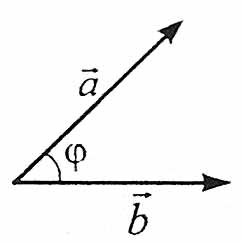
Отже, .

Кут між двома векторами зі спільним початком визначається, як і звичайний кут.

Якщо є два довільні вектори  і , то кутом між ними називається кут між рівними їм векторами зі спільним початком.

                     

Кут між спів напрямленими векторами вважається таким, що дорівнює нулю.

 11. Ознака перпендикулярності векторів

Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю.

І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.