Підготовка до ЗНО з математики. Алгебра.

     Означення. Число а більше числа b, якщо різниця а-b є числом додатним.

     Число а менше числа b, якщо різниця а-b є числом від’ємним.

     Якщо а більше b, то пишуть: а>b; якщо а менше b, то пишуть: а<b.

     Отже, нерівність а>b означає, що різниця а-b є додатною, тобто а-b>0; нерівність а<b означає, що різниця а-b є від’ємною, тобто а-b<0.

     Два вирази, які сполучені знаком > або <, називають строгими нерівностями.

     Знаки > і < є знаками строгої нерівності, вони протилежні один одному: якщо а>b, то b<а, і навпаки.

     Окрім знаків > і <, використовують також знаки:

≥ - більше або дорівнює (не менше),

≤ - менше або дорівнює (не більше).

     Невірність а≤b означає, що а<b або а=b, тобто а не більше b.

    Наприклад: якщо число учнів вашого класу 30,то число а учнів, які присутні на уроці, може бути меншим або дорівнювати 30. У цьому випадку можна записати: а≤30.

     Аналогічно нерівність а≥b означає, що а>b або а=b, тобто а не менше b.

     Два вирази, які сполучені знаком ≥ або ≤, називають нестрогими нерівностями. Знаки ≥ і ≤ є знаками нестрогої нерівності.

     Наведемо приклади нерівностей:

1)               6<5;                                        5) 2х+3>2;

2)               7<9;                                        6) 3х-1>2х+1;

3)               4≥4;                                        7) ${x^2} + x > 3$;

4)               4≥1;                                        8) $\sqrt 2 \le 1$.

     Вираз, який стоїть ліворуч або праворуч від знака нерівності, називають відповідно лівою чи правою частиною нерівності.

     Наприклад: лівою частиною нерівності ${x^2} + x > 3$ є вираз ${x^2} + x$, а правою число – 3.

     Якщо обидві частини нерівності – числа, то її називають числовою нерівністю.

     Такі нерівності бувають правильні або неправильні.

    Наприклад: нерівності 7<9; 4≥4; 4≥1 – правильні, а нерівності 5>6; $\sqrt 2 \le 1$ - неправильні.

    Теорема 1. Якщо а<b, b<с, то а<с.

     Геометрично ця властивість означає: якщо точка А (якій відповідає число а) лежить лівіше від точки В (якій відповідає число b), а точка В, у свою чергу, лежить лівіше від точки С (якій відповідає число с), тоді точка А тим більше буде лежати лівіше від точки С.

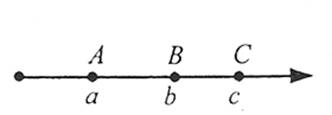
     Аналогічно, якщо а>b, b>с, то а>с.

    Теорема 2. Якщо а<b і с – будь-яке число, то а+с<b+с.

     Отже, якщо до обох частин правильної нерівності додати одне й те саме число, то отримаємо правильну нерівність.

     Аналогічно: якщо а>b і с – будь-яке число, то а+с>b+с.

     Наслідок. Будь-який доданок можна перенести з однієї частини нерівності в іншу, змінивши знак цього доданка на протилежний.

    Теорема 3. Якщо а<b і с>0, то ас<bс. Якщо а<b і с<0, то ас>bс.

     Аналогічно: а) якщо а>b і с>0, то ас>bс; б) якщо а>b і с<0, то ас<bс.

     Оскільки ділення можна замінити множенням на число, обернене до дільника, то аналогічні властивості є справедливими й для ділення:

а) якщо а<b і с>0, то $\frac{a}{c} < \frac{b}{c}$;

б) якщо а<b і с<0, то $\frac{a}{c} > \frac{b}{c}$.

     Отже, якщо обидві частини правильної нерівності помножити або поділити на одне й те саме додатне число, то отримаємо правильну нерівність.

     Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме від’ємне число і замінити знак нерівності на протилежний, то отримаємо правильну нерівність.

    Теорема 4. Якщо а>b і с>d, то а+с>b+d.

     Якщо почленно додати правильні нерівності одного знака, то одержимо правильну нерівність.

    Наприклад:

$1)\quad \frac{\begin{array}{l}3 > 2\\\;\; + \\7 > 1\end{array}}{\begin{array}{l}3 + 7 > 2 + 1\\\;\;\;10 > 3\end{array}};\quad 2)\quad \frac{\begin{array}{l}18 < 21\\\quad + \\17 < 20\end{array}}{\begin{array}{l}18 + 17 < 21 + 20\\\;\quad \;\;35 < 41\end{array}};\quad 3)\quad \frac{\begin{array}{l} - 1 < 6\\\quad \; + \\ - 7 < - 6\end{array}}{\begin{array}{l} - 1 - 7 < 6 - 6\\\quad \; - 8 < 0\end{array}}$

    Теорема 5. Якщо а<b, с<d і а>0, b>0, с>0, d>0, то ас<bd.

     Якщо почленно перемножити правильні нерівності одного знака, ліві і праві частини яких є додатними числами, то отримаємо правильну нерівність.

    Наприклад:

$1)\quad \frac{\begin{array}{l}3 < 4\\ \times \\5 < 6\end{array}}{\begin{array}{l}3 \cdot 5 < 4 \cdot 6\\\;\;15 < 24\end{array}};\quad 2)\quad \frac{\begin{array}{l}7 > 3\\ \times \\3 > 1\end{array}}{\begin{array}{l}7 \cdot 3 > 3 \cdot 1\\\;\;21 > 3\end{array}};\quad 3)\quad \frac{\begin{array}{l}x + y > x\\ \times \\x - y > y\end{array}}{\begin{array}{l}(x + y)(x - y) > xy\\\;\;\;\;{x^2} - {y^2} > xy\end{array}}$

     Слід зазначити, що теореми 4 і 5 справедливі для трьох і більше нерівностей.