Підготовка до ЗНО з математики. Алгебра.

     Нерівністю зі змінною (невідомим) називають два вирази зі змінною (невідомим), між якими стоїть один зі знаків нерівності: > (більше), < (менше), ≥ (більше або дорівнює; не менше); ≤ (менше або дорівнює; не більше).

    Наприклад: $3x + 2 > 6;{x^2} + x + 1 > 0$ - нерівності з однією змінною.

     Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює нерівність на правильну числову нерівність.

    Наприклад: число 2 – розв’язок нерівності х+3>4, а число -1 не є розв’язком даної нерівності.

    Приклад 2. Доведіть, що при кожному дійсному значенні а нерівність ${a^2} + 2 > 2a$ є справедливою.

Доведення

     Складемо різницю лівої і правої частин нерівностей й перетворимо її:

${a^2} + 2 - 2a = {a^2} - 2a + 1 + 1 = ({a^2} - 2a + 1) + 1 = {(a - 1)^2} + 1$.

     При будь-якому значенні а утворена різниця ${a^2} + 2 - 2a$ – додатна, тому що значення виразу ${(a - 1)^2}$ є невід’ємним, а значення виразу ${(a - 1)^2} + 1$ – додатним. Отже, при будь-якому значенні а нерівність ${a^2} + 2 > 2a$ є справедливою.

     Розв’язати нерівність з однією змінною означає знайти всі її розв’язки або довести, що розв’язків немає.

     Розв’язками нерівності є деяка множина чисел.

     У таблиці наведено деякі числові множини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності.

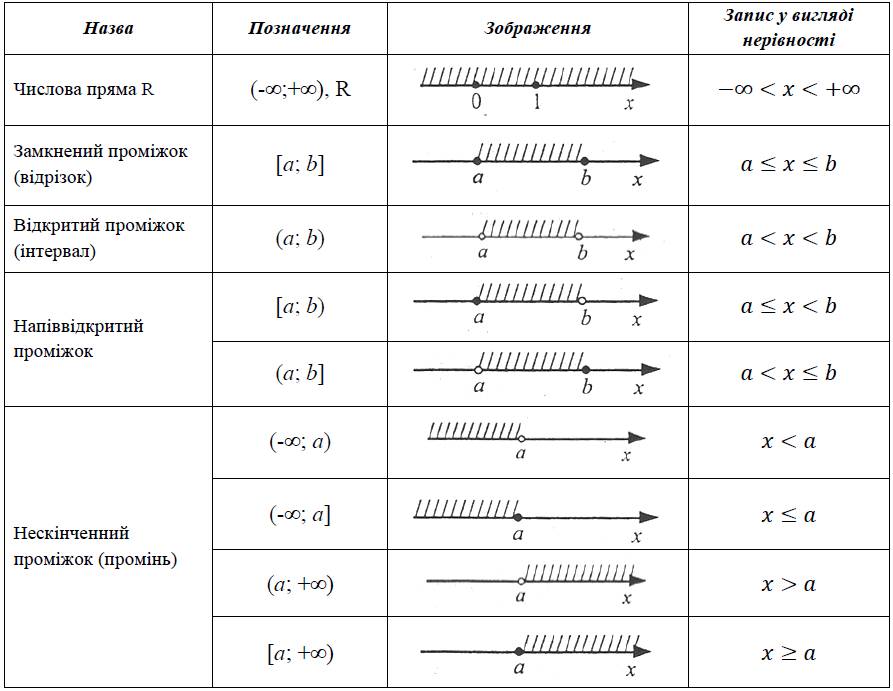
     Розв’язування нерівностей, як правило, зводиться до заміни даної нерівності нерівністю, яка їй рівносильна.

     Нерівності, які мають одні й ті самі розв’язки, називаються рівносильними. Нерівності, які не мають розв’язків, також вважаються рівносильними.

     Нерівності з однією змінною мають такі властивості:

     1. Якщо з однієї частини нерівності перенести в другу доданок із протилежним знаком, то одержимо рівносильну їй нерівність.

    Наприклад: нерівність х+2>3 рівносильна нерівності х+2-2>3-2, тобто х>1.

     2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то отримаємо рівносильну їй нерівність.

    Наприклад: $\frac{1}{2}x > 3$ рівносильна нерівності $\frac{1}{2}x \cdot 2 > 3 \cdot 2$, тобто х>6.

     3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши знак нерівності на протилежний, то одержимо рівносильну їй нерівність.

    Наприклад: нерівність -2х<10 рівносильна нерівності -2х:(-2)>10:(-2), тобто х>-5.

    Приклад 3. Розв’яжіть нерівність 2(х-5)+6≥9х-2(х-3).

Розв’язання

     Перетворимо ліву і праву частини нерівності, тобто розкриємо дужки:

2х-10+6≥9х-2х+6.

     Перенесемо члени, що містять змінну до лівої частини нерівності, а члени, які не містять змінну, у праву частину нерівності, при цьому змінимо знаки членів на протилежні:

2х-9х+2х≥10-6+6.

     Зведемо подібні в лівій і правій частинах нерівності:

-5х≥10.

     Поділимо обидві частини нерівності на -5, змінивши знак нерівності на протилежний:

х≤-2.

     Отже, розв’язком нерівності є проміжок (-∞;-2].

     Відповідь: (-∞;-2].