ФУНКЦІЇ ТА ЇХ ОСНОВНІ ВЛАСТИВОСТІ
5. Парні та непарні функції
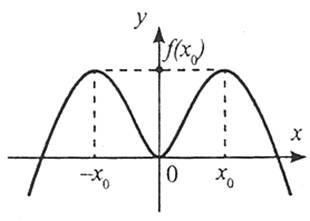
Функція  є парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність
є парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність  . Графік парної функції симетричний відносно осі ОY.
. Графік парної функції симетричний відносно осі ОY.
Приклад 1. Чи є парною функція  ?
?
Оскільки  і
і  , то функція парна.
, то функція парна.
Приклад 2. Чи є парною функція  ?
?
Оскільки  , але
, але  , то функція є непарною.
, то функція є непарною.
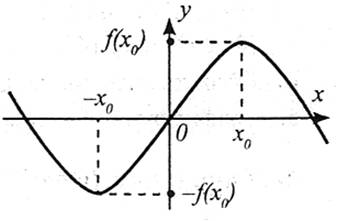
Функція  є непарною, якщо для будь-якого значення х із D(y) значення
є непарною, якщо для будь-якого значення х із D(y) значення  і виконується рівність
і виконується рівність  . Графік непарної функції симетричний відносно початку координат.
. Графік непарної функції симетричний відносно початку координат.
Приклад 3. Чи є непарною функція  ?
?
Оскільки  і
і  , то функція є непарною.
, то функція є непарною.

