Підготовка до ЗНО з математики. Алгебра.

     Числовою функцією з областю визначення D називають залежність, згідно з якою кожному числу х із множини D відповідає за деяким правилом єдине число у із множини Е.

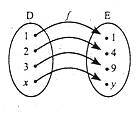
     Змінну х називають незалежною змінною або аргументом функції, а змінну у – залежною змінною або функцією.

     Функцію позначають латинськими буквами f, g, h,… (або f(x), g(x), h(x),…) або рівностями y=f(x), y=g(x), y=h(x),…

     Якщо задане конкретне значення незалежної змінної $x = {x_0}$, то ${y_0} = f({x_0})$ називається значенням функції f у точці ${x_0}$.

    Наприклад: якщо $f(x) = \frac{{{x^2}}}{{{x^2} + 1}}$, то $f(1) = \frac{{{1^2}}}{{{1^2} + 1}} = \frac{1}{2}$, $f(0) = \frac{{{0^2}}}{{{0^2} + 1}} = 0$, $f(a) = \frac{{{a^2}}}{{{a^2} + 1}}$.

     Область визначення функції позначають D(f). Множина, що складається з усіх чисел f(x) таких, що х належить області визначення функції f, називається областю значень функції і позначається Е(f).

     Розглянемо приклад. Результати вимірювання температури тіла хворого залежно від часу подано в таблиці:

     Залежність y=f(x) є функцією, де х – незалежна змінна, у – залежна змінна.

f(9)=39; f(12)=38,5; f(15)=38,3; f(18)=37,3; f(21)=37,1; f(24)=37.

D(f)={9; 12; 15; 18; 21; 24}.

Е(f)={39;38,5; 38,3; 37,3; 37,1; 37}.

     Функцію можна задати за допомогою таблиці, графіка, формули.

     Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу х.

    Наприклад: якщо кожному значенню х із множини дійсних чисел відповідає квадрат цього числа, то функцію можна записати у вигляді формули: $y = {x^2}$, або $f(x) = {x^2}$.

     Областю визначення функції у=f(х), яка задана формулою, називають множину тих значень, яких може набувати х, тобто таких х, за яких формула має зміст (усі дії, указані формулою, можна виконати).

     При знаходженні області визначення слід пам’ятати:

1. Якщо функція є многочленом $y = {a_n}{x^n} + {a_{n - 1}}{x^{n - 1}} + ... + {a_1}x + {a_0}$, то $D(y) = ( - \infty ; + \infty ) = R$.

    Наприклад: якщо $y = {x^2} + 2x + 1$, то $D(y) = R$.

2. Якщо функція має вигляд $y = \frac{{f(x)}}{{g(x)}}$, де $f(x),g(x)$ – многочлени, то слід вважати g(x)≠0 (знаменник дробу не дорівнює 0).

    Наприклад: якщо $y = \frac{x}{{{x^2} - 1}}$, то ${{x^2} - 1 \ne 0}$. Тоді х≠1 і х≠-1. Отже, $D(y) = ( - \infty ; - 1) \cup ( - 1;1) \cup (1; + \infty )$.

3. Якщо функція має вигляд $y = \sqrt {f(x)}$, то слід вважати f(x)≥0 (арифметичний квадратний корінь існує тільки з невід’ємних чисел).

    Наприклад: якщо $y = \sqrt {5 + x}$, то $5 + x \ge 0,x \ge - 5$, тобто $D(y) = [ - 5; + \infty )$.