Підготовка до ЗНО з математики. Алгебра.

Функція $y = kx$

     Властивості:

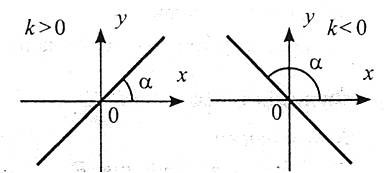
1. Область визначення: R.

2. Функція є непарною.

3. Для $x \in R$ функція зростає, якщо $k > 0$; спадає, якщо $k < 0$.

4. Область значень: R.

5. Графік – пряма, що проходить через початок координат.

Функція $y = b$

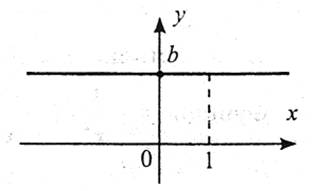
     Властивості:

1. Область визначення: R.

2. Функція є парною. Якщо b=0, то функція і парна, і непарна.

3. Для $x \in R$ функція стала.

4. Область значень: {b}.

5. Графік – пряма, паралельна осі х, якщо b≠0, і пряма, що збігається з віссю х, якщо b=0.

6. Функція періодична, будь-яке число є періодом. Найменшого додатного періоду немає.

Функція $y = \frac{k}{x}\;(y = \frac{k}{{{x^{2n + 1}}}},n \in N,k \ne 0)$

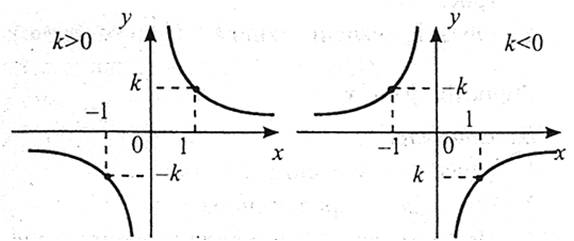
     Властивості

1. Область визначення: $x \in ( - \infty ;0) \cup (0; + \infty )$.

2. Функція є непарною.

3. Якщо $k > 0$, функція спадає на проміжку $( - \infty ;0)$ і на проміжку $(0; + \infty )$. Якщо $k < 0$, функція зростає на проміжку $( - \infty ;0)$ і на проміжку $(0; + \infty )$.

4. Область значень: $( - \infty ;0) \cup (0; + \infty )$.

5. Графік функції – гіпербола.

Функція $y = a{x^2}\;(y = a{x^{2n}},a \ne 0,n \in N)$

     Властивості

1. Область визначення: R.

2. Функція є парною.

3. Якщо $a > 0$, функція спадає на проміжку (-∞;0], зростає на проміжку [0;+∞). Якщо $a < 0$, функція зростає на проміжку (-∞;0], спадає на проміжку [0;+∞).

4. Область значень: якщо $a > 0$, то $y \in [0; + \infty )$; якщо $a < 0$, то $y \in ( - \infty ;0]$.

5. Графік функції – парабола.

Функція $y = a{x^3}\;(y = a{x^{2n + 1}},a \ne 0,n \in N)$

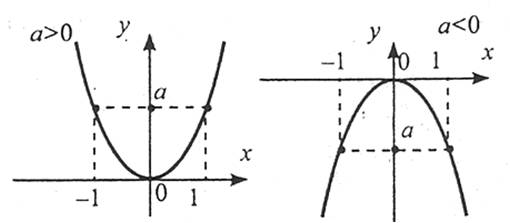
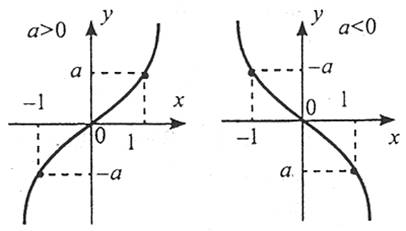
     Властивості

1. Область визначення: R.

2. Функція є непарною.

3. Для $x \in R$ функція зростає, якщо $a > 0$; спадає, якщо $a < 0$.

4. Область значень: R.

5. Графік функції – кубічна парабола.

Функція $y = |x|$

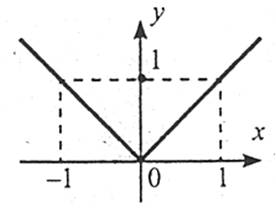
     Властивості

1. Область визначення: R.

2. Функція є парною.

3. На проміжку (-∞;0] функція спадає; на проміжку [0;+∞) функція зростає.

4. Область значень: [0;+∞).

Функція $y = \frac{k}{{{x^{2n}}}}\;(y = \frac{k}{{{x^{2n + 1}}}},k \ne 0,n \in N)$

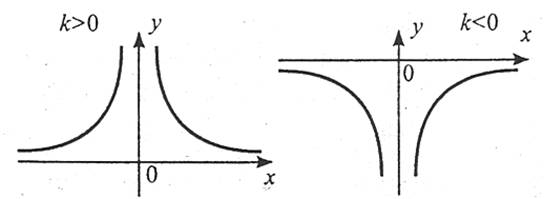
     Властивості

1. Область визначення: $x \in ( - \infty ;0) \cup (0; + \infty )$.

2. Функція є парною.

3. Якщо $k > 0$, функція зростає на проміжку $( - \infty ;0)$ і спадає на проміжку $(0; + \infty )$. Якщо $k < 0$, функція спадає на проміжку $( - \infty ;0)$ і зростає на проміжку $(0; + \infty )$.

4. Область значень: якщо $k > 0$, то $y \in (0; + \infty )$; якщо $k < 0$, то $y \in ( - \infty ;0)$.

Функція $y = \sqrt x$

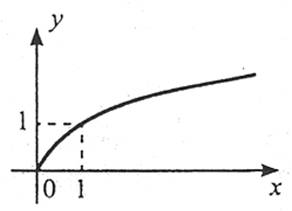
     Властивості

1. Область визначення: [0;+∞).

2. Функція ні парна, ні непарна.

3. На проміжку [0;+∞) функція зростає.

4. Область значень: [0;+∞).