ФУНКЦІЇ ТА ЇХ ОСНОВНІ ВЛАСТИВОСТІ
8. Функція, обернена до даної
Функцію, яка набуває кожного свого значення в єдиній точці області визначення, називають оборотною.
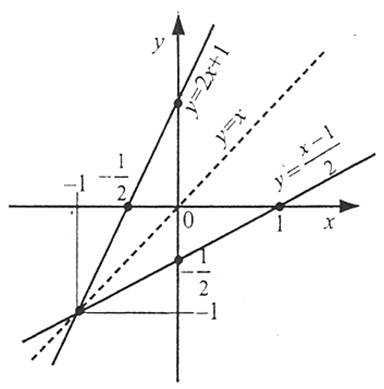
Наприклад: функція у=2х+1 – оборотна, а функція  (визначена на всій числовій осі) не є оборотною.
(визначена на всій числовій осі) не є оборотною.
Якщо функція задана формулою  , то для знаходження оберненої функції потрібно розв’язати рівняння
, то для знаходження оберненої функції потрібно розв’язати рівняння  відносно х, а потім поміняти місцями х і у.
відносно х, а потім поміняти місцями х і у.
Наприклад: оберненою до функції  є функція
є функція  .
.
Якщо рівняння  відносно х має більше ніж один корінь, то функція
відносно х має більше ніж один корінь, то функція  не має оберненої функції.
не має оберненої функції.
Наприклад: функція  оберненої функції не має.
оберненої функції не має.
Графіки даної функції і оберненої до неї симетричні відносно прямої у=х.
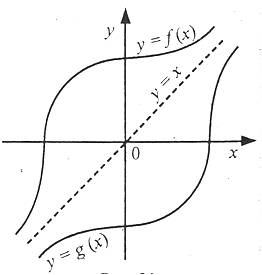
Наприклад: функції  , графіки яких симетричні відносно прямої у=х, є оберненими.
, графіки яких симетричні відносно прямої у=х, є оберненими.
Якщо функція  зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції
зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції  , також є зростаючою (спадною).
, також є зростаючою (спадною).
Якщо функція  визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D.
визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D.