ЛІНІЙНА ФУНКЦІЯ. ЛІНІЙНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
4. Системи лінійних рівнянь з двома змінними
Системи рівнянь розв’язують кількома способами: графічним, підстановки, додавання. Розглянемо приклади.
Приклад 7. Розв’яжіть систему рівнянь графічним способом
Розв’язання
Побудуємо графіки рівнянь х+у=5 або у=-х+5 (пряма, яка проходить через точки (0;5) і (5;0)) та х-у=1 або у=х-1 (пряма, яка проходить через точки (0;-1) та (1;0)).
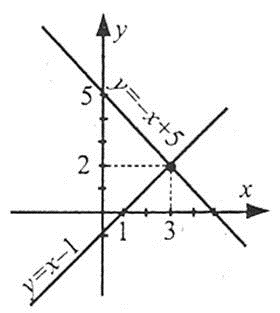
Ці графіки перетинаються в точці (3;2).
Отже, розв’язком системи є пара (3;2).
Відповідь: (3;2).
Щоб розв’язати систему рівнянь графічним способом, треба:
1. виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;
2. побудувати графіки;
3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв’язками (розв’язком) системи рівнянь.
Зауваження. Графічний спосіб розв’язування систем рівнянь не є універсальним, оскільки не завжди розв’язком системи є пара цілих чисел. Іноді важко точно встановити координати точки перетину побудованих графіків функцій, можливо лише вказати наближенні значення. Тому, як правило, використовують алгебрагічні способи розв’язування систем рівнянь: спосіб підстановки, додавання.
Приклад 8. Розв’яжіть систему рівнянь способом підстановки
Розв’язання
Із першого рівняння системи виразимо у через х: у=6-2х. одержаний вираз підставимо в друге рівняння системи:
4х-3(6-2х)=2, звідси 4х-18+6х=2; 10х=20; х=2.
Одержане значення х підставляємо у вираз у=6-2х;
у=6-2·2.
Отже, пара (2;2) – розв’язок даної системи.
Відповідь: (2;2).
Способом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком:
1. з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини;
2. знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;
3. розв’язуємо одержане рівняння і знаходимо значення цієї змінної;
4. підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення;
5. записуємо відповідь.
Зауваження. Спосіб підстановки, як правило, використовують, якщо коефіцієнт при одній зі змінних в одному з рівнянь системи дорівнює 1.
Приклад 9. Розв’яжіть систему рівнянь способом додавання
Розв’язання
Помножимо почленно перше рівняння системи на 3, а друге – на 2 (це дає змогу при додаванні рівнянь позбавитися від змінної у):
Додавши почленно рівняння, одержуємо 19х=19, звідси х=1 (значення у знайдемо з першого рівняння системи: 3·1+2у=5, 2у=2, у=1, отже, (1;1) – розв’язок системи).
Значення у можна знайти, якщо помножимо почленно перше рівняння на -5, а друге – на 3:
Додавши почленно рівняння, одержуємо:
-19у=-19, у=1.
Отже, пара (1;1) є розв’язком даної системи.
Відповідь: (1;1).
Розв’язування системи двох лінійних рівнянь із двома змінними способом алгебрагічного додавання виконують за таким порядком:
1) урівнюємо коефіцієнти при одній зі змінних шляхом по членного множення обох рівнянь на множники, підібрані відповідним чином;
2) додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну зі змінних;
3) розв’язуємо одержане рівняння з однією змінною;
4) значення другої змінної можна знайти таким же способом (або підстановкою знайденого значення змінної в будь-яке із заданих рівнянь системи);
5) записуємо відповідь.
Зауваження. Спосіб додавання, як правило, використовують, якщо коефіцієнти при одній зі змінних у рівнянні системи – протилежні числа.






