ТРИГОНОМЕТРИЧНІ І ОБЕРНЕНО ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ТА ЇХ ВЛАСТИВОСТІ
5. Функція y=arcctg x
Функція y=ctg x на проміжку  спадає і набуває всіх значень із R, тому для будь якого а рівняння ctg x=a має єдиний розв’язок із проміжку
спадає і набуває всіх значень із R, тому для будь якого а рівняння ctg x=a має єдиний розв’язок із проміжку  , який називають арккотангенсом числа а і позначають arсctg a.
, який називають арккотангенсом числа а і позначають arсctg a.
Арккотангенсом числа а називають таке число з проміжку  , котангенс якого дорівнює а.
, котангенс якого дорівнює а.
Графік функції y=arcсtg x одержимо із графіка функції y=сtg x,  , перетворенням симетрії відносно прямої у=х.
, перетворенням симетрії відносно прямої у=х.
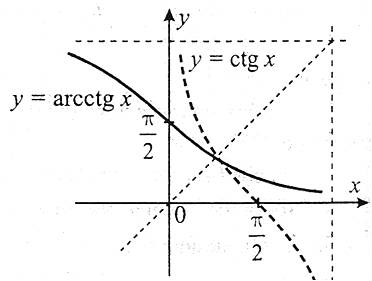
Основні властивості функції y=arcсtg x:
1. D(y)=R.
3. Графік не симетричний ані відносно початку координат, ані відносно осі OY: arcctg (-x)=π-arcctg x.
4. Функція спадна. Якщо х1<х2, то arсctg x1>arсctg x2.
Зауваження
При знаходженні області визначення треба пам’ятати якщо функція має вигляд y=ctg (f(x)), то слід вважати  (котангенс чисел
(котангенс чисел  , не визначений).
, не визначений).












