Степеневі функції та їх властивості. Ірраціональні рівняння, нерівності та їх системи
3. Ірраціональні нерівності
Для розв’язання ірраціональних нерівностей використовуємо узагальнений метод інтервалів. Розв’язком нерівності f(x)>0 (f(x)<0) можуть бути тільки числа, що входять в область визначення функції y=f(x). Розв’язком нерівності f(x)>0 є ті інтервали області визначення y=f(x), де ця функція є додатною. З’ясуємо яким чином довільна функція може змінити свій знак.
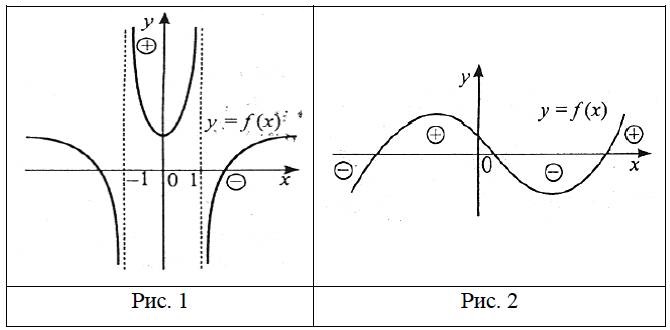
На рис. 1 і 2 зображено графіки двох функцій. На рис. 1 графік розривається в точках х=-1 та х=1 і знак функції змінюється при переході через точки -1 та 1. На рис. 2 знак функції змінюється при переході графіка з нижньої півплощини у верхню (і навпаки), тобто в тих точках, де графік перетинає вісь ОХ. На осі ОХ значення функції дорівнює нулю, тому значення аргументу, при яких функція дорівнює 0, називають нулями функції.
Отже, будь-яка функція може змінювати свій знак тільки в точках, де розривається графік функції, або в нулях.
Отже, щоб розв’язати нерівність f(x)>0 (f(x)<0), треба:
1) знайти область визначення функції y=f(x). (Коли ми знаходимо область визначення функції, то при цьому виділяються і точки, у яких розривається графік функції.);
2) знайти нулі функції (розв’язати рівняння f(x)=0);
3) на координатній прямій позначити нулі функції на області її визначення і визначити знак функції на кожному інтервалі, на які розбивають нулі функції область визначення (у кожному із цих інтервалів функція зберігає знак, і його можна визначити в будь-якій точці цього інтервалу);
4) записати відповідь (вибрати інтервали, де функція має потрібний знак).