Приклади розв'язування завдань
8. Приклад 8
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
Приведемо нерівність до вигляду  .
.
Уведемо функцію  і знайдемо х, при яких у<0. Для цього:
і знайдемо х, при яких у<0. Для цього:
1) знайдемо область визначення функції:
![]()
2) знайдемо нулі функції:
3) наносимо нуль функції на область її визначення. Знаходимо знак функції на кожному з трьох інтервалів, на які розбивається область визначення нулем функції, і записуємо відповідь.
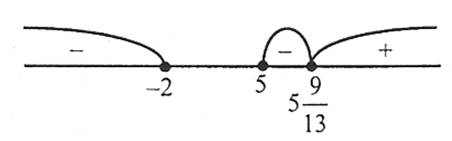
![(x + 2)(x - 5) \ge 0;\;D(y) = ( - \infty ; - 2] \cup [5; + \infty ) (x + 2)(x - 5) \ge 0;\;D(y) = ( - \infty ; - 2] \cup [5; + \infty )](http://zno.academia.in.ua/filter/tex/pix.php/ad686220fff3c290b8a9b137aaed060c.gif)






![( - \infty ; - 2] \cup [5;5\frac{9}{{13}}) ( - \infty ; - 2] \cup [5;5\frac{9}{{13}})](http://zno.academia.in.ua/filter/tex/pix.php/869cfaac3c89f26ef92d5b2eb2211bba.gif)