Підготовка до ЗНО з математики. Алгебра.

     Функцію виду $y = {\log _a}x$, де $a > 0,\;a \ne 1$, називають логарифмічною.

     Основні властивості логарифмічної функції

1. Область визначення – (0;+∞).
2. Область значень – множина всіх дійсних чисел R.
3. Якщо х=1, то у=0.
4. Функція $y = {\log _a}x$ не є ні парною, ні непарною.
5. Якщо а>1, функція $y = {\log _a}x$ зростає, а при 0<а<1 – спадає.
6. Якщо а>1 і х>1, то $y = {\log _a}x > 0$. Якщо а>1 і 0<х<1, то $y = {\log _a}x < 0$. Якщо 0<а<1 і х>1, то $y = {\log _a}x < 0$. Якщо 0<а<1 і 0<х<1, то $y = {\log _a}x > 0$.
7. Графік функції $y = {\log _a}x$:

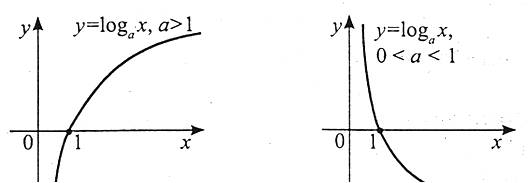
     При знаходженні області визначення слід пам’ятати:

1)               Якщо функція має вигляд $y = {\log _a}(f(x)),a > 1,a \ne 1$, то слід вважати f(x)>0 (під знаком логарифма може стояти тільки додатний вираз).

     Наприклад: якщо $y = \lg ({x^2} - 5x + 6)$, то ${x^2} - 5x + 6 > 0$, тобто $D(y) = ( - \infty ;2) \cup (3; + \infty )$.

2)               Якщо функція має вигляд $y = {\log _{f(x)}}b,b > 0$, то слід вважати

$\left\{ \begin{array}{l}f(x) > 0,\\f(x) \ne 1\end{array} \right.$

 (основа логарифма може бути тільки додатною і відмінною від одиниці).

     Наприклад: якщо $y = {\log _{x - 1}}10$, то 

$\left\{ \begin{array}{l}x - 1 > 0,\\x - 1 \ne 1,\end{array} \right.$

тобто $D(y) = (1;2) \cup (2; + \infty )$.