Приклади розв'язування завдань
Приклад 16
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
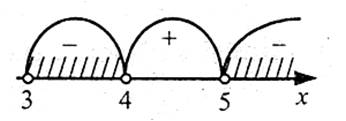
Нехай  і у<0. Область визначення функції знаходимо із системи:
і у<0. Область визначення функції знаходимо із системи:
Знайдемо нулі функції:
Значення х=2 не входить в область визначення функції. Зробивши перевірку, переконуємося, що х=5 – нуль функції.
Розіб’ємо область визначення функції на проміжки точкою 5 та знайдемо знаки функції на утворених проміжках.