Похідна та її застосування
Поняття екстремуму функції
При дослідженні поведінки функції в деякій точці зручно користуватися поняттям околу. Околом точки а називають будь-який інтервал, що містить цю точку.
Наприклад: інтервали (2; 5), (2,5; 3,5), (2,9; 3,1) – околи точки 3.
Розглянемо графік функції.
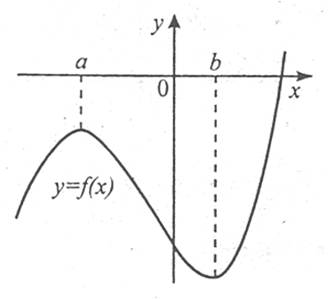
Як видно з рисунка, існує такий окіл точки х=а, що найбільше значення функції y=f(x) у цьому околі набуває в точці х=а. точку х=а називають точкою максимуму цієї функції.
Аналогічно точку х=b називають точкою мінімуму функції y=f(x), оскільки значення функції в цій точці найменше порівняно зі значеннями функції в деякому околі точки b.
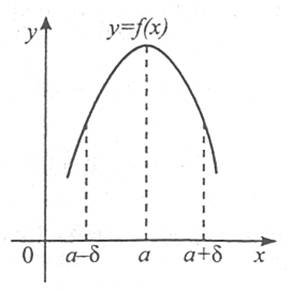
Означення. Точка а з області визначення функції f(x) називається точкою максимуму цієї функції, якщо існує такий окіл точки а, що для всіх х≠а із цього околу виконується нерівність f(x)<f(a).
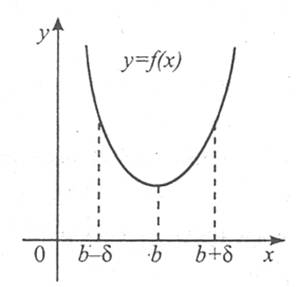
Означення. Точка b з області визначення функції f(x) називається точкою мінімуму цієї функції, якщо існує такий окіл точки b, що для всіх х≠b із цього околу виконується нерівність f(x)>f(b).
Точки максимуму і точки мінімуму називають точками екстремуму функції, а значення функції в цих точках – екстремумами функції (максимум і мінімум функції).
Точки максимуму позначають хmax, а точки мінімуму – хmin. Значення функції в цих точках, тобто максимуми і мінімуми, позначають відповідно уmаx і ymin.