Похідна та її застосування
Достатня умова зростання (спадання) функції на проміжку
Відомо, що функцію y=f(x) називають зростаючою на деякому проміжку, якщо для будь-яких х1 і х2, що належать проміжку, з умови х2>х1 випливає, що f(x2)>f(x1).
Дотична в кожній точці графіка зростаючої функції, утворює з додатним напрямом осі ОХ або гострий кут, або кут, що дорівнює нулю (в останньому випадку дотична є паралельною осі ОХ).
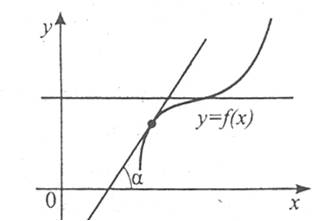
Виходячи з геометричного змісту похідної,  . Це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова
. Це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова
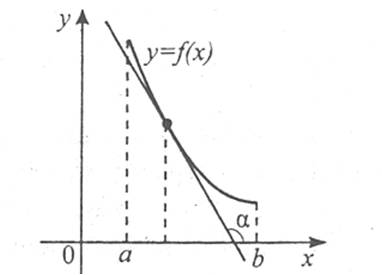
Функцію y=f(x) називають спадною на проміжку, якщо для будь-яких х1 і х2, що належать проміжку, з умови х2>х1 випливає, що f(x2)<f(x1). Дотична в кожній точці графіка спадної функції, утворює з віссю ОХ або тупий кут, або кут, що дорівнює нулю, тому для функції f(x), яка спадає на деякому проміжку, виконується умова
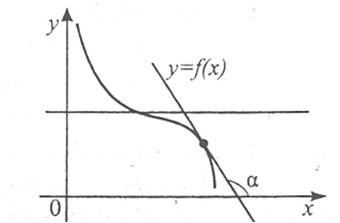
Одна й та сама функція може на одному проміжку області її визначення зростати, а на іншому – спадати. Характер поведінки функції на кожному із цих проміжків визначається знаком її похідної.
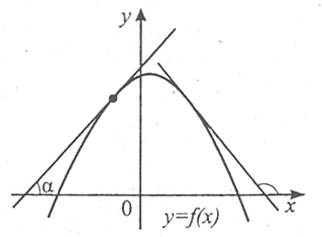
Отже, наочне уявлення дозволяє сформулювати властивості зростаючих та спадних функцій.
Якщо функція y=f(x) диференційована і зростає на деякому проміжку, то її похідна на цьому проміжку невід’ємна.
Якщо функція y=f(x) диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку недодатна.
Проте для розв’язування задач особливо важливими є обернені твердження, які виражають ознаки зростання і спадання функції на проміжку. Нехай значення похідної функції y=f(x) додатні на деякому проміжку, тобто  . Оскільки
. Оскільки  , то з умови tg α>0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути з додатним напрямом осі ОХ. У цьому випадку графік функції «піднімається» на заданому проміжку, тобто функція зростає.
, то з умови tg α>0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути з додатним напрямом осі ОХ. У цьому випадку графік функції «піднімається» на заданому проміжку, тобто функція зростає.
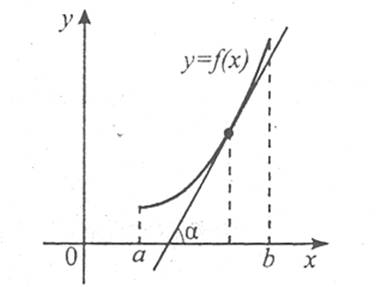
Якщо  на деякому проміжку, то кутовий коефіцієнт дотичної
на деякому проміжку, то кутовий коефіцієнт дотичної  до графіка функції y=f(x) від’ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ тупий кут і графік функції на даному проміжку «опускається», тобто функція f(x) спадає.
до графіка функції y=f(x) від’ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ тупий кут і графік функції на даному проміжку «опускається», тобто функція f(x) спадає.
Якщо  на проміжку, то функція f(x) зростає на цьому проміжку.
на проміжку, то функція f(x) зростає на цьому проміжку.
Якщо  на проміжку, то функція f(x) спадає на цьому проміжку.
на проміжку, то функція f(x) спадає на цьому проміжку.
Ці два твердження називають ознаками зростання (спадання) функції на проміжку.
Проміжки зростання і спадання функції часто називають проміжками монотонності цієї функції.

