Похідна та її застосування
Необхідна умова екстремуму
Розглянемо функцію y=f(x), яка визначена в деякому околі точки х0 і має похідну в цій точці.
Якщо х0 – точка екстремуму диференційованої функції y=f(x), то  .
.
Це твердження називають теоремою Ферма на честь французького математика П’єра Ферма (1601 – 1665).
Теорема Ферма має наочний геометричний зміст: у точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт  дорівнює нулю.
дорівнює нулю.
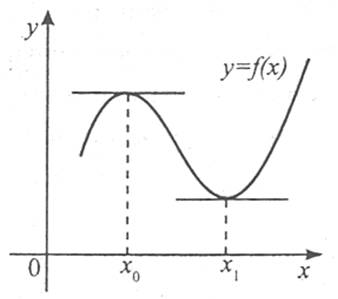
Наприклад: функція  має в точці х0=0 мінімум, її похідна
має в точці х0=0 мінімум, її похідна  .
.
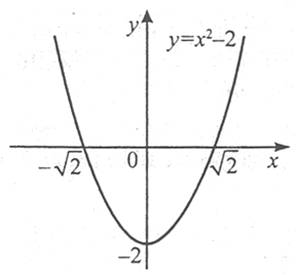
Функція  має максимум в точці х0=0,
має максимум в точці х0=0,  .
.
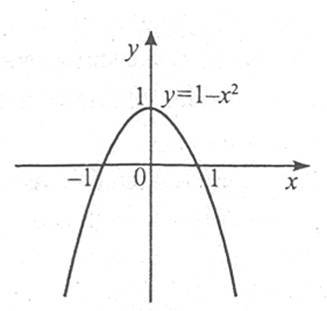
Слід зазначити, що якщо  , то х0 необов’язково є точкою екстремуму.
, то х0 необов’язково є точкою екстремуму.
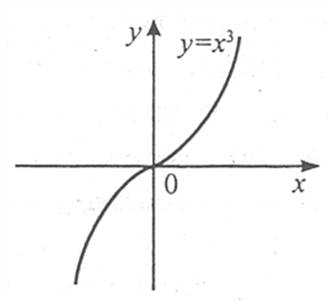
Наприклад: якщо  , то
, то  і
і  . Проте точка х=0 не є точкою екстремуму, оскільки функція
. Проте точка х=0 не є точкою екстремуму, оскільки функція  зростає на всій числовій осі.
зростає на всій числовій осі.
Отже, точки екстремуму диференційованої функції треба шукати тільки серед коренів рівняння  , але не завжди корінь рівняння
, але не завжди корінь рівняння  є точкою екстремуму.
є точкою екстремуму.
Внутрішні точки області визначення функції y=f(x), у яких похідна дорівнює нулю, називають стаціонарними. Отже, для того щоб точка х0 була точкою екстремуму, необхідно, щоб вона була стаціонарною.
Сформулюємо достатні умови для того, щоб стаціонарна точка була точкою екстремуму, тобто умови, при виконанні яких стаціонарна точка є точкою максимуму або мінімуму функції.
Якщо похідна ліворуч стаціонарної точки додатна, а праворуч – від’ємна, тобто при переході через цю точку похідна змінює знак із «+» на «-», то ця стаціонарна точка є точкою максимуму.
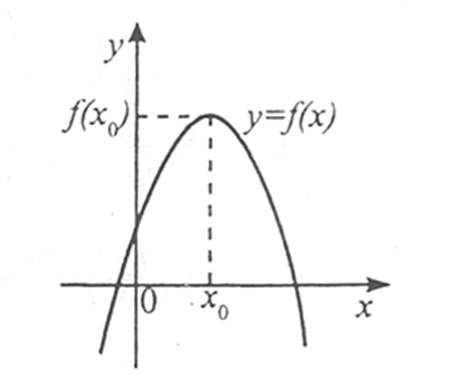
Дійсно, у цьому разі ліворуч стаціонарної точки функція зростає, а праворуч – спадає, отже, дана точка є точкою максимуму.
Якщо похідна ліворуч стаціонарної точки від’ємна, а праворуч – додатна, тобто при переході через стаціонарну точку похідна змінює знак із «-» на «+», то ця стаціонарна точка є точкою мінімуму.
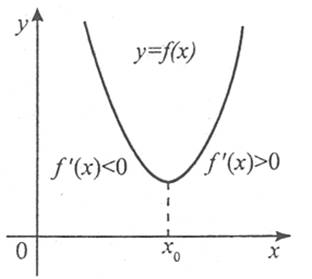
Якщо при переході через стаціонарну точку похідна не змінює знака, тобто ліворуч і праворуч від стаціонарної точки похідна додатна або від’ємна, то ця точка не є точкою екстремуму.