Похідна та її застосування
Найбільше і найменше значення функції на проміжку
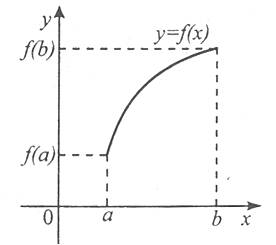
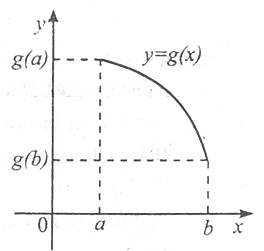
Розглянемо рис. 1 і 2, на яких зображено графіки функцій y=f(x) і y=g(x), заданих на відрізку [a; b].
|
|
|
|
Рис. 1 |
Рис. 2 |
Функція y=f(x) зростає, а функція y=g(x) спадає. На відрізку [a; b] найменше значення функції y=f(x) дорівнює f(a), а найменше значення функції y=g(x) дорівнює g(b). Відповідно найбільші значення цих функцій на даному відрізку дорівнюють f(b) та g(a). Отже, якщо функція непевна і зростає (спадає) на деякому відрізку, то найбільшого і найменшого значень функція набуває на кінцях цього відрізка.
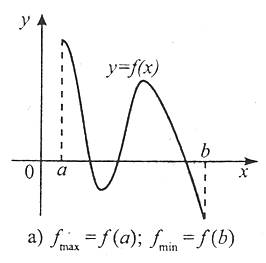
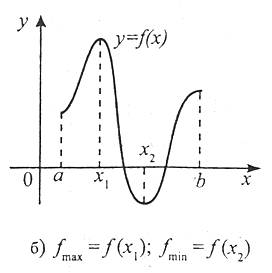
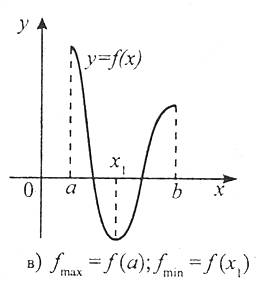
Розглянемо рис. 3, на якому зображено графіки трьох функцій. Аналіз цих графіків свідчить, що найбільше і найменше значення функцій неперервних і диференційованих на відрізку [a; b] досягаються цими функціями, або на кінцях відрізка, або в стаціонарних точках.
|
|
|
|
|
Рис. 3 |
||
Отже, неперервна і диференційована функція на заданому відрізку набуває найбільшого і найменшого значень у стаціонарних точках або на кінцях відрізка.