Підготовка до ЗНО з математики. Алгебра.

     Крім градусної міри, існує радіанна міра вимірювання кутів. Одиницею радіанної міри кутів є радіан.

     Кут величиною 1 радіан – це кут із вершиною в центрі кола, що спирається на дугу кола, довжина якого дорівнює радіусу цього кола.

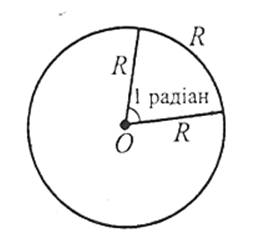
     Оскільки довжина півкола радіуса R дорівнює πR, то розгорнутий кут дорівнює π радіан, оскільки $\frac{{\pi R}}{R} = \pi$. Градусна міра розгорнутого кута дорівнює 180°, тому π=180°. Звідси $1rad = \frac{{180^\circ }}{\pi } = 57^\circ 17'45''$. Отже, зі співвідношення π=180° можна переходити від градусів до радіанів і навпаки. Зокрема, $1^\circ  = \frac{\pi }{{180^\circ }} = 0,017rad$.

     Розглянемо приклади переходу від радіанної міри до градусної і навпаки.

    Приклад 1. Виразіть у радіанах величини кутів 30°; 45°; 60°; 90°.

     Розділивши ліву і праву частини рівності 180°=π рад послідовно на 6, 4, 3, 2, одержуємо:

$30^\circ = \frac{\pi }{6}rad;45^\circ = \frac{\pi }{4}rad;60^\circ = \frac{\pi }{3}rad;90^\circ = \frac{\pi }{2}rad$.

    Приклад 2. Виразіть у градусах величини кутів  рад,  рад,  рад,  рад.

     Розділивши ліву і праву частини рівності 180°=π рад послідовно на 10; 5; 12; 18, одержуємо:

$\frac{\pi }{{10}}$ рад=18°; $\frac{\pi }{{5}}$ рад=36°; $\frac{\pi }{{12}}$ рад=15°; $\frac{\pi }{{18}}$ рад=10°.

     При записі радіанної міри кута позначення «рад» опускають.

    Наприклад: замість рівності 90°= $\frac{\pi }{2}$ рад, пишуть 90°= $\frac{\pi }{2}$.

     Радіанна міра кута зручна для обчислення довжини дуги кола. Через те, що кут величиною 1 радіан стягує дугу, довжина якої дорівнює R, кут величиною α радіан стягує дугу довжиною: l=αR.

Якщо радіус кола дорівнює одиниці, то l=α, тобто довжина дуги дорівнює величині центрального кута, що спирається на цю дугу, в радіанах.