Підготовка до ЗНО з математики. Геометрія.

Кутом між прямою та площиною називається кут між прямою та її проекцією на площину.

Наприклад: якщо φ – кут між прямою та площиною, то 0°≤φ≤90°.

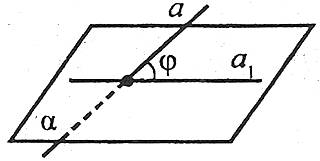
Кутом між похилою та площиною називається кут між похилою та її проекцією на дану площину.

Наприклад: якщо φ – кут між похилою та площиною, то 0°<φ<90°.

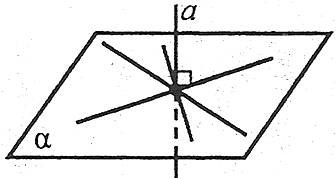
Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, яка лежить у цій площині. Перпендикулярність прямої а та площини α позначається так: .

Наприклад: пряма а перпендикулярна до площини α.

Властивості перпендикулярних прямої та площини

1. Якщо дві прямі перпендикулярні до однієї і тієї ж площини, то ці прямі паралельні.

Наприклад: якщо , то .

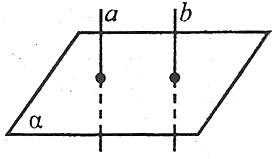
2. Якщо площина перпендикулярна до однієї з двох паралельних прямих,  то вона перпендикулярна до іншої.

Наприклад: якщо , то .

3. Якщо пряма перпендикулярна до однієї із двох паралельних площин, то вона перпендикулярна й до іншої.

Наприклад: якщо , то .

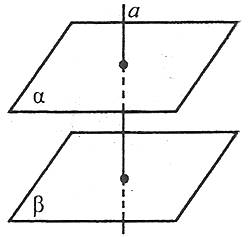
4. Якщо дві різні площини перпендикулярні до однієї і тієї самої прямої, то ці площини паралельні.

Наприклад: якщо , то .

Перпендикуляром, проведеним із даної точки на дану площину, називається відрізок, який з’єднує дану точку з точкою площини та лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається основою перпендикуляра.

Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який з’єднує дану точку з точкою площини та не є перпендикуляром до площини. Кінець цього відрізка, який лежить у площині, називається основою похилої.

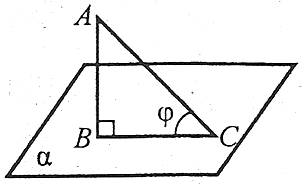
Відрізок, який з’єднує основи перпендикуляра та похилої, проведених з однієї і тієї ж точки, називається проекцією похилої на площину.

Наприклад: АВ – перпендикуляр до площини α, АС – похила до площини α, ВС – проекція похилої АС на площину α, В – основа перпендикуляра, С – основа похилої.

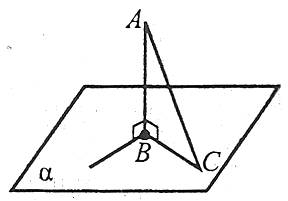
Якщо з даної точки проведено перпендикуляр та похилу, то перпендикуляр коротший за похилу.

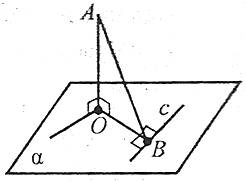
Теорема про три перпендикуляри

Якщо пряма, яка лежить у площині, перпендикулярна до проекції похилої на цю площину, то вона перпендикулярна і до самої похилої. І навпаки: якщо пряма, яка лежить у площині, перпендикулярна до похилої, то вона перпендикулярна і до самої проекції на цю площину.

Наприклад: АО – перпендикуляр, АВ – похила, ОВ – проекція похилої, с – пряма площини. Якщо , то , і навпаки: якщо , то . Пряма с може і не перетинатися з похилою АВ.