Піраміди, їх види та властивості
1. Піраміди
Пірамідою (n-кутною) називається многогранник, у якого одна грань є довільним n-кутником, а інші n граней – трикутники, які мають спільну вершину. N-кутник називається основою, а трикутники – бічними гранями. Спільна вершина бічних граней називається вершиною піраміди.
Наприклад: піраміда SABCD, ABCD – основа; 
– бічні грані піраміди; S – вершина піраміди; SA, SB, SC, SD – бічні ребра.
Висотою піраміди називається перпендикуляр, проведений із вершини піраміди на площину основи.
Наприклад: SO – висота піраміди.
Правильною називається піраміда, в основі якої лежить правильний многокутник, а висота піраміди співпадає з центром цього многокутника.
Висота бічної грані правильної піраміди, проведеної із вершини піраміди, називається її апофемою.
Наприклад: правильна трикутна піраміда SABC, 
, SK – апофема.
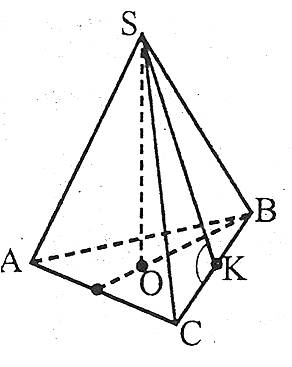
У правильній піраміді:
- бічні ребра рівні;
- бічні грані рівні;
- апофеми рівні;
- двогранні кути при основі рівні;
- двогранні кути при бічних ребрах рівні;
- кожна точка висоти правильної піраміди рівновіддалена від усіх вершин основи;
- кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней;
- кожна точка висоти правильної піраміди рівновіддалена від усіх бічних ребер.
Діагональним перерізом піраміди називається переріз площиною, яка проходить через два бічних ребра піраміди, що не належать одній грані.