КВАДРАТИЧНА ФУНКЦІЯ. КВАДРАТНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
7. Розв’язування квадратичних нерівностей методом інтервалів
Розглянемо розв’язування квадратичних нерівностей методом інтервалів на прикладі.
Приклад 1. Знайдіть, при яких значення х квадратний тричлен  набуває додатних значень, а при яких – від’ємних.
набуває додатних значень, а при яких – від’ємних.
Розв’язання
Розкладемо квадратний тричлен  на множники
на множники
Тоді х=2 і х=3 поділяють числову пряму на три проміжки: (-∞;2); (2;3); (3;+∞).
![]()
Вираз (х-2)(х-3) є добутком двох множників. Знак кожного з цих множників та їх добутку подамо у вигляді таблиці.
|
|
(-∞;2) |
(2;3) |
(3;+∞) |
|
х-2 |
- |
+ |
+ |
|
х-3 |
- |
- |
+ |
|
(х-2)(х-3) |
+ |
- |
+ |
Рухаючись уздовж числової осі зліва направо, ми бачимо, що на проміжку (-∞;2) тричлен  набуває додатних значень, оскільки в цьому випадку обидва множники х-2 і х-3 є від’ємними.
набуває додатних значень, оскільки в цьому випадку обидва множники х-2 і х-3 є від’ємними.
На проміжку (2;3) цей тричлен набуває від’ємних значень і, отже, при переході через точку х=2 змінює знак. Це відбувається тому, що в добутку (х-2)(х-3) при переході через точку х=2 перший множник х-2 змінює знак, а другий множник х-3 – ні.
При переході через точку х=3 тричлен знову змінює знак, оскільки в добутку (х-2)(х-3) перший множник х-2 не змінює знак, а другий множник х-3 змінює.
Отже, рухаючись уздовж числової прямої, ми спостерігаємо, як змінюється знак добутку (х-2)(х-3).
Таким чином, задачу про знак квадратного тричлена  можна розв’язувати у такий спосіб.
можна розв’язувати у такий спосіб.
Позначити на числовій прямій корені рівняння  , тобто точки х=2, х=3. Вони поділяють числову пряму на три проміжки. На проміжку (-∞;2) значення тричлена
, тобто точки х=2, х=3. Вони поділяють числову пряму на три проміжки. На проміжку (-∞;2) значення тричлена  додатне, тому розставляємо його знаки на останніх проміжках, ураховуючи чергування знаків.
додатне, тому розставляємо його знаки на останніх проміжках, ураховуючи чергування знаків.
![]()
На рис. видно, що  на проміжку
на проміжку  , а на проміжку (2;3) -
, а на проміжку (2;3) -  .
.
Приклад 2. Розв’яжіть нерівність  .
.
Розв’язання
Знайдемо корені квадратного тричлена  :
:
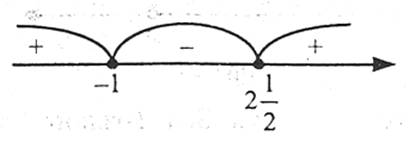
Наносимо на числову пряму точки -1 та  , які поділяють її на три проміжки. Визначаємо знак тричлена
, які поділяють її на три проміжки. Визначаємо знак тричлена  на проміжку (-∞;-1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.
на проміжку (-∞;-1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.

![( - \infty ; - 1] \cup [2\frac{1}{2}; + \infty ) ( - \infty ; - 1] \cup [2\frac{1}{2}; + \infty )](http://zno.academia.in.ua/filter/tex/pix.php/02a9839c7d5a798a5557717ce6e44ee7.gif)